Question

In a random sample of 400 residents of Boston, 320 residents indicated that they voted for Obama in the last presidential election. Develop a 95% confidence interval estimate for the proportion of all Boston residents who voted for Obama.

Answer 1

C.I = 0.7608 ≤ p ≤ 0.8392

Explanation:

Given that:

Let consider a random sample n = 400 candidates where 320 residents indicated that they voted for Obama

probability
`\hat p = (320)/(400)`

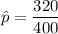
= 0.8

Level of significance ∝ = 100 -95%

= 5%

= 0.05

The objective is to develop a 95% confidence interval estimate for the proportion of all Boston residents who voted for Obama.

The confidence internal can be computed as:

`=\hat p \pm Z_(\alpha/2) \sqrt{( p(1-p))/(n ) }`

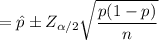
where;

`Z_(0.05/2)` =
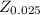`Z_(0.025)` = 1.960

SO;

`=0.8 \pm 1.960 \sqrt{( 0.8(1-0.8))/(400 ) }`

`=0.8 \pm 1.960 \sqrt{( 0.8(0.2))/(400 ) }`

`=0.8 \pm 1.960 \sqrt{( 0.16)/(400 ) }`

`=0.8 \pm 1.960 \sqrt{4 * 10^(-4)}`

`=0.8 \pm 1.960 * 0.02}`

`=0.8 \pm 0.0392`

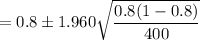
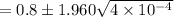
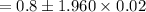
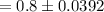
= 0.8 - 0.0392 OR 0.8 + 0.0392

= 0.7608 OR 0.8392

Thus; C.I = 0.7608 ≤ p ≤ 0.8392