Question

If mZNOM = 30°, then what is the length of the minor arc
NM?

Answer 1

Answer: C

Explanation:

4#/12 = #

Answer 2

Option (B)

Explanation:

To determine the length of arc of a circle we use the formula,

Length of arc =
`(\theta)/(360)(2\pi r)`

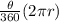
Where θ = measure of the central angle subtended by the arc

r = radius of the circle

For the circle given in the picture attached,

Length of arc NM =
`(30)/(360)(2\pi)(2)`

=
`(4\pi )/(12)`

=
`(\pi )/(3)`

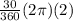
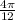
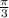
Therefore, length of
`\widehat{NM}=(\pi )/(3)`

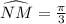
Option (B) will be the answer.