Question

Hypothesis Testing

Problem 1. Adults saving for retirement
In a recent survey conducted by Pew Research, it was found that 156 of 295 adult Americans without a high school diploma were worried about having enough saved for retirement. Does
the sample evidence suggest that a majority of adult Americans without a high school diploma are worried about having enough saved for retirement? Use a 0.05 level of significance
1. State the null and alternative hypothesis.
2. What type of hypothesis test is to be used?
3. What distribution should be used and why?
4. Is this a right, left, or two-tailed test?
5. Compute the test statistic.
6. Compute the p-value.
7. Do you reject or not reject the null hypothesis? Explain why.
8. What do you conclude?
Problem 2: Google Stock
Google became a publicly traded company in August 2004. Initially, the stock traded over 10 million shares each day! Since the initial offering, the volume of stock traded daily has
decreased substantially. In 2010, the mean daily volume in Google stock was 5.44 million shares, according to Yahoo!Enance. A random sample of 35 trading days in 2014 resulted in a
sample mean of 3.28 million shares with a standard deviation of 1.68 million shares. Does the evidence suggest that the volume of Google stock has changed since 2007? Use a 0.05 level of
significance
1. State the null and alternative hypothesis.
2. What type of hypothesis test is to be used?
3. What distribution should be used and why?
4. Is this a right, left, or two-tailed test?
5. Compute the test statistic.
6. Compute the p-value.
7. Do you reject or not reject the null hypothesis? Explain why
8. What do you conclude?

Answer 1

Problem 1: We conclude that less than or equal to 50% of adult Americans without a high school diploma are worried about having enough saved for retirement.

Problem 2: We conclude that the volume of Google stock has changed.

Explanation:

Problem 1:

We are given that in a recent survey conducted by Pew Research, it was found that 156 of 295 adult Americans without a high school diploma were worried about having enough saved for retirement.

Let p = proportion of adult Americans without a high school diploma who are worried about having enough saved for retirement

So, Null Hypothesis,
`H_0` : p
`\leq` 50% {means that less than or equal to 50% of adult Americans without a high school diploma are worried about having enough saved for retirement}

Alternate Hypothesis,
`H_A` : p > 50% {means that a majority of adult Americans without a high school diploma are worried about having enough saved for retirement}

This is a right-tailed test.

The test statistics that would be used here is One-sample z-test for proportions;

T.S. =
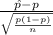`\frac{\hat p-p}{\sqrt{(p(1-p))/(n) } }` ~ N(0,1)

where,
`\hat p` = sample proportion of adult Americans who were worried about having enough saved for retirement =
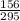`(156)/(295)` = 0.53

n = sample of adult Americans = 295

So, the test statistics =
`\frac{0.53-0.50}{\sqrt{(0.50(1-0.50))/(295) } }`

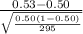
= 1.03

The value of z-test statistics is 1.03.

Also, the P-value of the test statistics is given by;

P-value = P(Z > 1.03) = 1 - P(Z
`\leq` 1.03)

= 1 - 0.8485 = 0.1515

Now, at a 0.05 level of significance, the z table gives a critical value of 1.645 for the right-tailed test.

Since the value of our test statistics is less than the critical value of z as 1.03 < 1.645, so we insufficient evidence to reject our null hypothesis as it will not fall in the rejection region.

Therefore, we conclude that less than or equal to 50% of adult Americans without a high school diploma are worried about having enough saved for retirement.

Problem 2:

We are given that a random sample of 35 trading days in 2014 resulted in a sample mean of 3.28 million shares with a standard deviation of 1.68 million shares.

Let
`\mu` = mean daily volume in Google stock

So, Null Hypothesis,
`H_0` :
`\mu` = 5.44 million shares {means that the volume of Google stock has not changed}

Alternate Hypothesis,
`H_A` :
`\mu`
`\\eq` 5.44 million shares {means that the volume of Google stock has changed}

This is a two-tailed test.

The test statistics that would be used here is One-sample t-test statistics because we don't know about the population standard deviation;

T.S. =
`(\bar X-\mu)/((s)/(√(n) ) )` ~
`t_n_-_1`

where,
`\bar X` = sample mean volume in Google stock = 3.28 million shares

s = sample standard deviation = 1.68 million shares

n = sample of trading days = 35

So, the test statistics =
`(3.28-5.44)/((1.68)/(√(35) ) )` ~
`t_3_4`

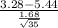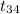
= -7.606

The value of t-test statistics is -7.606.

Also, the P-value of the test statistics is given by;

P-value = P(
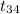`t_3_4` < -7.606) = Less than 0.05%

Now, at a 0.05 level of significance, the t table gives a critical value of -2.032 and 2.032 at 34 degrees of freedom for the two-tailed test.

Since the value of our test statistics doesn't lie within the range of critical values of t, so we sufficient evidence to reject our null hypothesis as it will fall in the rejection region.

Therefore, we conclude that the volume of Google stock has changed.