Question

Find the perimeter and the area of each shape. Give your answer as a completely simplified exact value in terms of π (no approximations).

Answer 1

Circumference: 12π + 8 cm,

Area: 48 ( cm )^2

Explanation:

This figure is composed of circles, squares, and semicircles. As you can see, the squares indicate that each semicircle should have ( 1 ) the same area, and ( 2 ) the same length ( circumference ). It would be easier to take the circumference of the figure first, as it is composed of arcs part of semicircles the same length.

Circumference of 1 semicircle =
`(1)/(2)`( πd ) =
`(1)/(2)`π( 4 ) = 2π ( cm )

Circumference of Figure (composed of 6 semicircles + 2 sides of a square),

We know that 6 semicircles should be 6
`*` 2π, and as the sides of a square are equal - if one side is 4 cm, the other 3 are 4 cm as well. Therefore the " 2 sides of a square " should be 2

Circumference of Figure = 6
`*` 2π + 2 = 12π + 8 ( cm )

_____________

The area of this figure is our next target. As you can see, it is composed of 3 semicircles, and the area of 3 semicircles subtracted from the area of 3 squares. Therefore, let us calculate the area of 1 semicircle, and the area of 1 square first.

Area of 1 semicircle = 1/2π
`r^2` = 1/2π
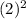`(2)^2` = 2π ( cm ),

Area of 1 square = ( 4 cm )( 4 cm ) = 16 (
`cm^2` )

So, the area of the figure should be the following -

Area of Figure = 3
`*` 2π + 3( 16 - 2π ) = 48 ( cm )^2