Answer:
(a) The probability that the sample mean will be more than 61 pounds is 0.0069.
(b) The probability that the sample mean will be more than 57 pounds is 0.4522.
(c) The probability that the sample mean will be between 55 and 58 pounds is 0.6112.
(d) The probability that the sample mean will be less than 55 pounds is 0.14686.
(e) The probability that the sample mean will be less than 48 pounds is 0.00001.
Explanation:
We are given that the Aluminum Association reports that the average American uses 56.8 pounds of aluminum in a year.
A random sample of 51 households is monitored for one year to determine aluminum usage. Also, the population standard deviation of annual usage is 12.2 pounds.
Let
 = sample mean
= sample mean
The z-score probability distribution for the sample mean is given by;
Z =
 ~ N(0,1)
~ N(0,1)
where,
 = average aluminum used by American = 56.8 pounds
= average aluminum used by American = 56.8 pounds
 = population standard deviation = 12.2 pounds
= population standard deviation = 12.2 pounds
n = sample of households = 51
(a) The probability that the sample mean will be more than 61 pounds is given by = P(
 > 61 pounds)
> 61 pounds)
P(
 > 61 pounds) = P(
> 61 pounds) = P(
 >
>
 ) = P(Z > 2.46) = 1 - P(Z
) = P(Z > 2.46) = 1 - P(Z
 2.46)
2.46)
= 1 - 0.9931 = 0.0069
The above probability is calculated by looking at the value of x = 2.46 in the z table which has an area of 0.9931.
(b) The probability that the sample mean will be more than 57 pounds is given by = P(
 > 57 pounds)
> 57 pounds)
P(
 > 57 pounds) = P(
> 57 pounds) = P(
 >
>
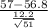 ) = P(Z > 0.12) = 1 - P(Z
) = P(Z > 0.12) = 1 - P(Z
 0.12)
0.12)
= 1 - 0.5478 = 0.4522
The above probability is calculated by looking at the value of x = 0.12 in the z table which has an area of 0.5478.
(c) The probability that the sample mean will be between 55 and 58 pounds is given by = P(55 pounds <
 < 58 pounds)
< 58 pounds)
P(55 pounds <
 < 58 pounds) = P(
< 58 pounds) = P(
 < 58 pounds) - P(
< 58 pounds) - P(

 55 pounds)
55 pounds)
P(
 < 58 pounds) = P(
< 58 pounds) = P(
 <
<
 ) = P(Z < 0.70) = 0.75804
) = P(Z < 0.70) = 0.75804
P(

 55 pounds) = P(
55 pounds) = P(


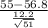 ) = P(Z
) = P(Z
 -1.05) = 1 - P(Z < 1.05)
-1.05) = 1 - P(Z < 1.05)
= 1 - 0.85314 = 0.14686
The above probability is calculated by looking at the value of x = 0.70 and x = 1.05 in the z table which has an area of 0.75804 and 0.85314.
Therefore, P(55 pounds <
 < 58 pounds) = 0.75804 - 0.14686 = 0.6112.
< 58 pounds) = 0.75804 - 0.14686 = 0.6112.
(d) The probability that the sample mean will be less than 55 pounds is given by = P(
 < 55 pounds)
< 55 pounds)
P(
 < 55 pounds) = P(
< 55 pounds) = P(
 <
<
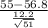 ) = P(Z < -1.05) = 1 - P(Z
) = P(Z < -1.05) = 1 - P(Z
 1.05)
1.05)
= 1 - 0.85314 = 0.14686
The above probability is calculated by looking at the value of x = 1.05 in the z table which has an area of 0.85314.
(e) The probability that the sample mean will be less than 48 pounds is given by = P(
 < 48 pounds)
< 48 pounds)
P(
 < 48 pounds) = P(
< 48 pounds) = P(
 <
<
 ) = P(Z < -5.15) = 1 - P(Z
) = P(Z < -5.15) = 1 - P(Z
 5.15)
5.15)
= 1 - 0.99999 = 0.00001
The above probability is calculated by looking at the value of x = 5.15 in the z table which has an area of 0.99999.