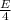Question

A narrow copper wire of length L and radius b is attached to a wide copper wire of length L and radius 2b, forming one long wire of length 2L. This long wire is attached to a battery, and a current is flowing through it. If the electric field in the narrow wire is E, the electric field in the wide wire is

Answer 1

electric field in the wide wire is

E₂ =
`(E)/(4)`

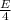
Step-by-step explanation:

given

length of the copper wire = L

radius of the copper wire r₁ = b

length of the second copper wire = L

radius of the second copper wire r₂ = 2b

electric field in the narrow wire = E₁=E

recall

resistance R = ρL/A

where ρ is resistivity of the copper wire, L is the length, and A is the cross sectional area.

Resistance of narrow wire, R₁

R₁ = ρL/A

where A = πb²

R₁ = ρL/πb²---------- eqn 1

Resistance of wide wire, R₂

R₂ = ρL/A

where A = π(2b)²

R₂ = ρL/π(2b)²

R₂ = ρL/4πb²-------------- eqn 2

R₂ = ¹/₄(ρL/πb²)

comparing eqn 1 and 2

R₁ = 4R₂

calculating the current in the wire,

I = E/(R₁ + R₂)

recall

R₁ = 4R₂

∴ I = E/(4R₂ + R₂)

I = E/5R₂

calculating the potential difference across R₁ & R₂

V₁ = IR₁

I = E/5R₂

∴ V₁ = ER₁/5R₂

R₁ = 4R₂

V₁ = 4ER₂/5R₂

∴V₁ = ⁴/₅E

potential difference for R₂

V₂= IR₂

I = E/5R₂

∴ V₂ = ER₂/5R₂

V₂ = ER₂/5R₂

∴V₂ = ¹/₅E

so, electric field E = V/L

for narrow wire E₁ = V₁/L ----------- eqn 3

for wide wire, E₂ = V₂/L------------ eqn 4

compare eqn 3 and 4

E₂/E₁ = V₂/V₁( L is constant)

E₂/E₁ = ¹/₅E/⁴/₅E

E₂ = E₁/4

note E₁ = E

∴E₂ =
`(E)/(4)`