Question

Given: XY - tangent to circles k1(P) and k2(O) OX=16, PY=6 and OP=26 Find: XY

Answer 1

XY = 24 units

Explanation:

First of all, we need to some construction here.

Let us draw a line parallel to XY from point P towards OX, which cuts OX at point Q.

Please refer to the attached figure.

Now, Let us consider triangle OQP which is a right angled triangle, with

Hypotenuse, OP = 26 units

Height, OQ = OX - PY = 16 - 6 = 10 units

Base, PQ = ?

We can use pythagorean theorem here to find the value of PQ.

According to pythagorean theorem:

`\text{Hypotenuse}^(2) = \text{Base}^(2) + \text{Perpendicular}^(2)\\\Rightarrow OP^(2) = PQ^(2) + OQ^(2)\\\Rightarrow 26^(2) = OQ^(2)+10^(2) \\\Rightarrow PQ^(2) = 26^(2)-10^(2) \\\Rightarrow PQ^(2) = 676-100 \\\Rightarrow PQ^(2) = 576\\\Rightarrow PQ= 24\ units`

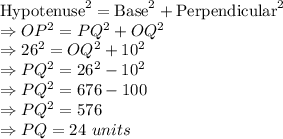
Now, we can see that side PQ is equal to side XY.

`\therefore` XY = 24 units is the answer.