Question

Air enters a 28-cm diameter pipe steadily at 200 kPaand 208C with a velocity of 5 m/s. Air is heated as it flows, and leaves the pipe at 180 kPa and 408C. Determine (a) the volume flow rate of air at the inlet, (b) the mass flow rate of air, and(c) the velocity and volume flow rate at the exit.

Answer 1

(a)
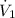`\dot V_1` = 0.308 m³/s

(b)
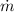`\dot m` = 0.732 kg/m³

(c) v₂ = 5.94 m/s.

Step-by-step explanation:

(a) The volume flow rate is given by the cross sectional area of the pipe × Velocity of flow of air

Diameter of pipe = 28 cm = 0.28 m

The cross sectional area, A, of the pipe = 0.28²/4×π = 0.0616 m²

Volume flow rate = 5 × 0.0616 = 0.308 m³/s

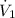`\dot V_1` = 0.308 m³/s

(b) From the general gas equation, we have;

p₁v₁ = RT₁ which gives;

p₁/ρ₁ = RT₁

ρ₁ = p₁/(RT₁)

Where:

ρ₁ = Density of the air

p₁ = 200 kPa

T₁ = 20 C =

R = 0.287 kPa·m³/(kg·K)

ρ₁ = 200/(0.287 ×293.15) = 2.377 kg/m³

The mass flow rate = Volume flow rate × Density

The mass flow rate,
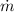`\dot m` = 2.377×0.308 = 0.732 kg/m³

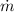`\dot m` = 0.732 kg/m³

(c) The density at exit, ρ₂, is found from the the universal gas equation as follows;

ρ₂ = p₂/(RT₂)

Where:

p₂ = Pressure at exit = 180 kPa

T₂ = Exit temperature = 40°C = 273.15 + 40 = 313.15 K

∴ ρ₂ = 180/(0.287×313.15) = 2.003 kg/m³

`\dot m` = ρ₂×
`\dot V_2`

`\dot V_2` =
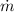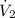
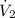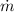`\dot m`/ρ₂ = 0.732/2.003 = 0.366 m³/s

`\dot V_2` = v₂ × A

v₂ =
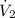`\dot V_2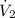`/A = 0.366/0.0616 = 5.94 m/s.

v₂ = 5.94 m/s.