Question

Colossus Added to six flags st. Louis in 1986, the Colossus is a giant Ferris wheel. Its diameter is 165 feet, it rotates at a rate of about 1.6 revolutions per minute, and the bottom of the wheel is 15 feet above the ground. Determine an equation that relates a rider's height the ride at the bottom of the wheel.

Answer 1

Given:

D=165 feet and the frequency of the motion is 1.6 revolutions per minute.

Solution:

The radius is half of the diameter.

The radius of the wheel is 82.5 feet.

`T=(1)/(1.6) \text{ minutes}`

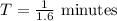
As we know:
`\omega=(2\pi)/(T)`

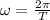
Substitute the value of T in the above formula.

`\omega=(2\pi)/((1)/(1.6))\\\omega=3.2\pi`

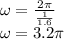
If the center of the wheel is at the origin then for
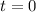`t=0` the rest position is
`-a`.

This can be written as:

`h(t)=-a\cos(\omega t)\\h(t)=-82.5cos(32.\pi t)`

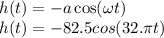
The actual height of the rider from the ground is:

`h(t)=\text{ Initial height from bottom}+\text{ radius}-82.5\cos(3.2\pi t)\\h(t)=15+82.5-82.5\cos(3.2\pi t)\\h(t)=97.5-82.5\cos(3.2\pi t)`

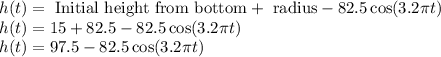
The required equation is
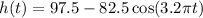`h(t)=97.5-82.5\cos(3.2\pi t)`.