Question

A motorcycle travels up one side of a hill over the top and down the other side. The crest of the hill can be considered to be a circular arc with radius of 45.0 m. Determine the maximum speed that the cycle can have while moving over the crest without losing contact with the road.

Answer 1

The maximum speed of the motorcycle should be 21 m/s

Step-by-step explanation:

Since the hill is considered to be a circular arc, the motorcycle will experience centripetal force that tends to flip it away from the center of the hill.

Since the motorcycle does not lose contact with the ground, it means that the weight of the motorcycle downwards just balances the centripetal force on the motorcycle.

we know that the centripetal force on the motorcycle is equal to

centripetal force =
`(mv^(2) )/(r)`

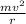
where m is the mass of the motorcycle,

v is the velocity of the motorcycle,

and r is the radius of the hill = 45.0 m

Also we now that the weight of the motorcycle is equal to

weight = mg

where m is still the mass of the motorcycle,

and g is the acceleration due to gravity = 9.81 m/s

Equating the both forces since they are equal, we'll have

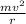`(mv^(2) )/(r)` = mg

the mass of the motorcycle will cancel out, and we'll be left with

`v^(2) = gr`

`v = √(gr)`

`v = √(9.81*45)`

`v = √(441.45)`

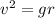
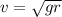
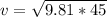
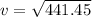
`v` = 21 m/s