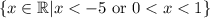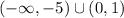Answer:
Interval notation is
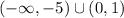
Solutions:
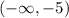
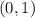
Explanation:
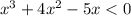
In this inequality, luckly we can easily factor it.
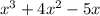
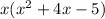
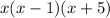
So we have
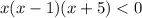
In exercises of this kind I usually do in my mind, but just to make it clear, let's do a table to organize. This table represents the x-intercepts in order to evaluate the inequality.
Consider
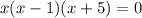 . Here, those are the possible values for
. Here, those are the possible values for
 for each factor to be 0:
for each factor to be 0:
The first step to complete the table is the x value where the factor will be equal to zero.






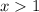
 0
0
 0
0
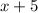 0
0
Then, just consider the signal:






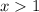
 - - - 0 + + +
- - - 0 + + +
 - - - - - 0 +
- - - - - 0 +
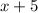 - 0 + + + + +
- 0 + + + + +
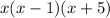 - 0 + 0 - 0 +
- 0 + 0 - 0 +
When
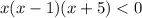 ?
?
It happens when
 and when
and when

The solution is