Answer:
0.9168
Explanation:
From the data given:
Mean = 110
standard deviation = 5
Let consider a random sample n =49 which have a mean between 109 and 112.
The test statistics can be computed as:
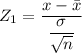
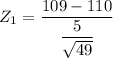
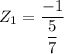
 = -1.4
= -1.4
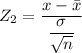
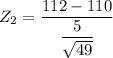
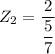

Thus; P(109 <
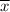 < 112) = P( - 1.4 < Z < 2.8)
< 112) = P( - 1.4 < Z < 2.8)
= P(Z < 2.8) - P( Z < -1.4)
= 0.9974 - 0.0806
= 0.9168