Question

A disk-shaped merry-go-round of radius 3.03 mand mass 145 kg rotates freely with an angular speed of 0.681 rev/s . A 65.4 kg person running tangential to the rim of the merry-go-round at 3.41 m/s jumps onto its rim and holds on. Before jumping on the merry-go-round, the person was moving in the same direction as the merry-go-round's rim. What is the final angular speed of the merry-go-round?

Answer 1

`\omega_2=0.891\ rev/s`

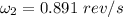
Step-by-step explanation:

Given that

Radius , r= 3.03 m

Mass of disk , M= 145 kg

Initial angular velocity

ω=0.681 rev/s

Mass of person , m= 65.4 kg

Velocity of person , V= 3.41 m/s

Initial mass moment of inertia

`I_1= (M* R^2)/(2)`

`I_1= (145* 3.03^2)/(2)=665.61\ kg.m^2`

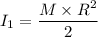
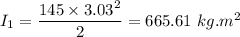
Final mass moment of inertia

`I_2= (M* R^2)/(2)+m* R^2`

`I_2= (145* 3.03^2)/(2)+65.4* 3.03^2=1266.04\ kg.m^2`

`Final\ angular\ velocity =\omega_2`

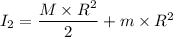
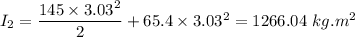
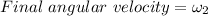
By using angular momentum equation

`I_1* \omega+m* V* R=I_2* \omega_2`

`665.61* 0.681+65.4* 3.41* 3.03=1266.04* \omega_2`

`1129.01= 1266.04* \omega_2`

`\omega_2=(1129.01)/(1266.04)`

`\omega_2=0.891\ rev/s`

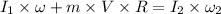
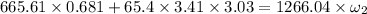
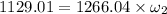
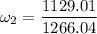
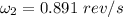
Thus the angular velocity will be 0.891 rev/s