Question

1) Suppose f(x) = x2 and g(x) = |x|. Then the composites (fog)(x) = |x|2 = x2 and (gof)(x) = |x2| = x2 are both differentiable at x = 0 even though g itself is not differentiable at x = 0. Does this contradict the chain rule? Explain.

Answer 1

This contradict of the chain rule.

Explanation:

The given functions are

`f(x)=x^2`

`g(x)=|x|`

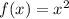
It is given that,

`(f\circ g)(x)=|x|^2=x^2`

`(g\circ f)(x)=|x^2|=x^2`

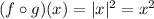
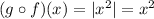
According to chin rule,

`(f\circ g)(c)=f(g(c))=f'(g(c)g'(c)`

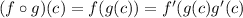
It means,
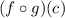`(f\circ g)(c)` is differentiable if f(g(c)) and g(c) is differentiable at x=c.

Here g(x) is not differentiable at x=0 but both compositions are differentiable, which is a contradiction of the chain rule