Question

An unbiased coin is tossed 14 times. In how many ways can the coin land tails either exactly 9 times or exactly 3 times?

Answer 1

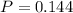`P= 0.144` ways

the coin can land tails either exactly 8 times or exactly 5 times in

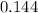`0.144` ways

Step by step explanation:

THis is a binomial distribution

Binomial distribution gives summary of the number of trials as well as observations as each trial has the same probability of attaining one particular value.

P(9)=(14,9).(0.5)⁹.(0.5)¹⁴⁻⁹

p(3)=(14,3).(0.5)⁹.(0.5)¹⁴⁻³

p=(9)+p(3)

p=C(14,9)(0.5)¹⁴ + C(14,3). (0.5)¹⁴

P= (0.5)¹⁴ [C(14,9) + C(14,3)]

P= (0.5)¹⁴ [2002 * 364]

P= 1/16384 * (2002 +364)

P= 91091/2048

P= 0.144

Hence,the coin can land tails either exactly 8 times or exactly 5 times in

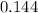`0.144` ways