Question

Find the equation for a hyperbola centered at (0, 0), with foci at (0,-sqrt73)) and (0,-sqrt73)) and vertices at (0, -8) and (0, 8).

Answer 1

`(y^2)/(64)-(x^2)/(9)=1` .

Explanation:

Since vertices lie on y-axis. So, it is a vertical parabola of the form

`((y-k)^2)/(a^2)-((x-h)^2)/(b^2)=1`

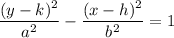
where, (h,k) is center,
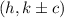`(h,k\pm c)` is focus and
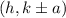`(h,k\pm a)` is vertex.

Center is (0,0). So, h=0 and k=0.

Foci are
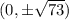`(0,\pm √(73))`. So
`c=√(73)`.

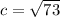Vertices are
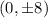`(0,\pm 8)`. So
`a=8`.

We know that,

`a^2+b^2=c^2`

`8^2+b^2=(√(73))^2`

`b^2=73-64`

`b=3`

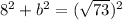
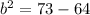
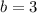
Put h=0,k=0, a=8 and b=3 in equation (1).

`((y-0)^2)/(8^2)-((x-0)^2)/(3^2)=1`

`(y^2)/(64)-(x^2)/(9)=1`

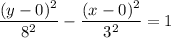
Therefore, the required equation is
`(y^2)/(64)-(x^2)/(9)=1` .