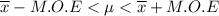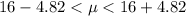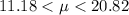Question

A meteorologist who sampled 4 thunderstorms found that the average speed at which they traveled across a certain state was 16 miles per hour. The standard deviation of the sample was 4.1 miles per hour. Round the final answers to at least two decimal places.

Required:
Find the 90% confidence interval of the mean. Assume the variable is normally distributed.

Answer 1

`11.18 < \mu <20.82`

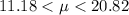
Explanation:

From the information given:

A meteorologist who sampled 4 thunderstorms of the sample size n = 16

the average speed at which they traveled across a certain state was 16 miles per hour ; i.e Mean
`\bar x` = 16

The standard deviation
`\sigma` of the sample was 4.1 miles per hour

The objective is to find the 90% confidence interval of the mean.

To start with the degree of freedom df = n - 1

degree of freedom df = 4 - 1

degree of freedom df = 3

At 90 % Confidence interval C.I ; the level of significance will be ∝ = 1 - C.I

∝ = 1 - 0.90

∝ = 0.10

∝/2 = 0.10/2

∝/2 = 0.050

From the tables;

Now the t value when ∝/2 = 0.050 is
`t_(\alpha / 2 ,df)`

`t_(0.050 \ ,\ 3) = 2.353`

The Margin of Error =
`t_(\alpha / 2 ,df) * (s)/(√(n))`

The Margin of Error =
`2.353 * (4.1)/(√(4))`

The Margin of Error =
`2.353 * (4.1)/(2)`

The Margin of Error =
`2.353 * 2.05`

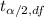
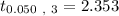
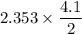
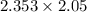
The Margin of Error = 4.82365

The Margin of Error = 4.82

Finally; Assume the variable is normally distributed, the 90% confidence interval of the mean is;

`\overline x - M.O.E < \mu < \overline x + M.O.E`

`16 -4.82 < \mu < 16 + 4.82`

`11.18 < \mu <20.82`

Answer 2

The 90 % confidence interval for the mean population is (11.176 ; 20.824 )

Rounding to at least two decimal places would give 11.18 , 20.83

Explanation:

Mean = x`= 16 miles per hour

standard deviation =s= 4.1 miles per hour

n= 4

`(s)/(\sqrt n)` = 4.1/√4= 4.1/2= 2.05

1-α= 0.9

degrees of freedom =n-1= df= 3

∈ ( estimator t with 90 % and df= 3 from t - table ) 2.353

Using Students' t - test

x`±∈ *
`(s)/(\sqrt n)`

Putting values

16 ± 2.353 * 2.05

= 16 + 4.82365

20.824 ; 11.176

The 90 % confidence interval for the mean population is (11.176 ; 20.824 )

Rounding to at least two decimal places would give 11.18 , 20.83