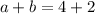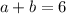Answer:
The sum is 6
Explanation:
Given
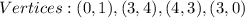
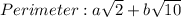
Required
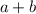
The first step is to name each points, as follows
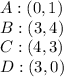
Next is to calculate the distance between each consecutive point
We'll calculate the distance AB, BC, CD and DA
Distance between points is calculated as thus;
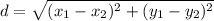
Calculating distance AB
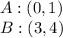
Here,
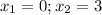
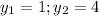


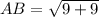

Expand 18 as 9 * 2
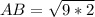
Split surds
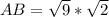
Take square root of 9

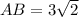
Calculating distance BC
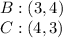
Here,

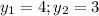
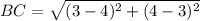
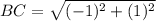
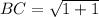

Calculating distance CD
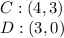
Here,
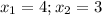
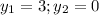

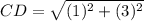

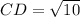
Calculating distance CD
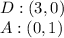
Here,
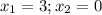
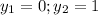
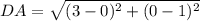
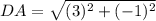

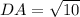
At this point, the perimeter can then be calculated
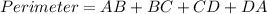
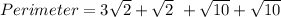
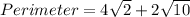
From the given parameters;
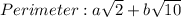
This implies that;

By comparison;
a = 4 and b = 2
Hence;