Answer:
a + b = 12
Explanation:
Given
Quadrilateral;
Vertices of (0,1), (3,4) (4,3) and (3,0)
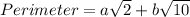
Required
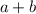
Let the vertices be represented with A,B,C,D such as
A = (0,1); B = (3,4); C = (4,3) and D = (3,0)
To calculate the actual perimeter, we need to first calculate the distance between the points;
Such that:
AB represents distance between point A and B
BC represents distance between point B and C
CD represents distance between point C and D
DA represents distance between point D and A
Calculating AB
Here, we consider A = (0,1); B = (3,4);
Distance is calculated as;
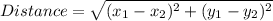
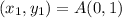

Substitute these values in the formula above
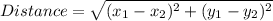

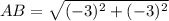


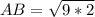
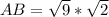
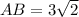
Calculating BC
Here, we consider B = (3,4); C = (4,3)
Here,
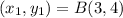

Substitute these values in the formula above
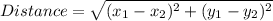
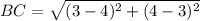
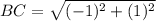
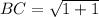

Calculating CD
Here, we consider C = (4,3); D = (3,0)
Here,
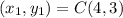
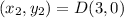
Substitute these values in the formula above
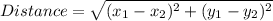

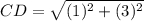

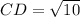
Lastly;
Calculating DA
Here, we consider C = (4,3); D = (3,0)
Here,
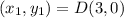
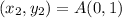
Substitute these values in the formula above
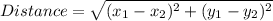
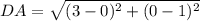
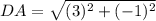

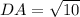
The addition of the values of distances AB, BC, CD and DA gives the perimeter of the quadrilateral
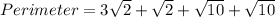

Recall that
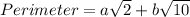
This implies that
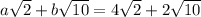
By comparison
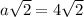
Divide both sides by

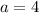
By comparison
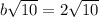
Divide both sides by
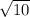
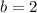
Hence,
a + b = 2 + 10
a + b = 12