Question

Type the correct answer in each box. Use numerals instead of words. If necessary, use / for the fraction bar. The endpoints of AB are A(1,4) and B(6,-1). If point C divides AB in the ratio 2 : 3, the coordinates of point C are (_,_). If point D divides AC in the ratio 3 : 2, the coordinates of point D are (_,_). help plz!

Answer 1

3,2 and 2.2,2.8

Explanation:

got a 100 on plato

Answer 2

- The coordinates of C is (3,2)

- The coordinates of D is (11/5,14/5)

Explanation:

Given

A(1,4) and B(6,-1)

Required

a. Point C divide AB in ratio 2:3

b. Point D divide AC in ratio 3:2

When endpoints are divided into ratios, the formula to calculate the coordinates is;

`(x,y) = ((mx_2 + nx_1)/(m+n),(my_2 + ny_1)/(m+n))`

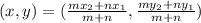
Solving for (a): Point C divide AB in ratio 2:3

The ratio;

`m : n = 2 : 3`

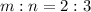
For Point A;

`A(x_1,y_1) = (1,4)`

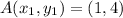
For Point B;

`B(x_2,y_2) = (6,-1)`

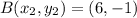
Substitute m,n,x1,x2,y1,y2 in the ratio formula given above;

`C(x,y) = ((mx_2 + nx_1)/(m+n),(my_2 + ny_1)/(m+n))`

`C(x,y) = ((2 * 6 + 3 * 1)/(3+2),(2 *-1 + 3 * 4)/(3+2))`

`C(x,y) = ((12 + 3 )/(5),\frac{-2 + 12}5})`

`C(x,y) = ((15 )/(5),\frac{10}5})`

`C(x,y) = (3,2)`

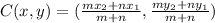
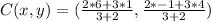
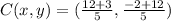
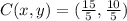
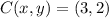
The coordinates of C is (3,2)

Solving for (b): Point D divide AC in ratio 3:2

Using the same steps as (a) above;

The ratio;

`m : n = 3:2`

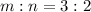
For Point A;

`A(x_1,y_1) = (1,4)`

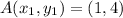
For Point C;

`C(x_2,y_2) = (3,2)`

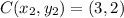
Substitute m,n,x1,x2,y1,y2 in the folowing ratio formula;

`D(x,y) = ((mx_2 + nx_1)/(m+n),(my_2 + ny_1)/(m+n))`

`C(x,y) = ((3 * 3 + 2 * 1)/(2+3),(3 *2 + 2 * 4)/(2+3))`

`D(x,y) = ((9 + 2)/(5),(6 + 8)/(5))`

`D(x,y) = ((11)/(5),(14)/(5))`

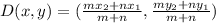
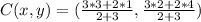
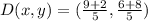
The coordinates of D is (11/5,14/5)