Question

The monthly starting salaries of students who receive an MBA degree have a standard deviation of $110. What size sample should be selected to obtain a 0.95 probability of estimating the mean monthly income within $20 or less

Answer 1

116.21

Explanation:

Using the formula for calculating margin error to tackle the question.

Margin error =
`(Z \sigma)/(√(n) )`

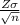
Z is the value at 95% confidence

`\sigma` is the standard deviation

n is the sample size to be estimated

Since the mean monthly income is within $20 or less, our margin error will be $20

Given
`\sigma` = $110, Z value at 95% confidence = 1.96 we can calculate the sample side n.

Making n the subject of the formula from the equation above;

`M.E = (Z \sigma)/(√(n) )\\\\√(n) = (Z \sigma)/(M.E ) \\\\`

`n = ((Z \sigma)/(M.E ))^(2)`

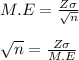
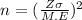
Substituting the give value into the resulting expression;

`n = ((1.96 * 110)/(20))^(2)\\\\n = ((215.6)/(20)) ^2\\\\n = 10.78^2\\\\n = 116.21`

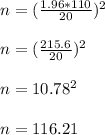
This shows that the sample size that should be selected to obtain a 0.95 probability of estimating the mean monthly income within $20 or less is approximately 116.21