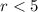Question

Simplify: |3r−15| if r<5

Answer 1

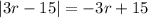`|3r-15| = -3r+15` if
`r<5`

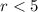
Explanation:

Given that:

r < 5

To simplify:

|3r−15|

Solution:

First of all, let us learn about Modulus function:

`f(x) =|x| =\left \{ {x, \ if\ {x>0} \atop -x\ if\ {x<0}} \right.`

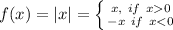
In other words, we can say:

Modulus function has a role to make its contents positive.

If the contents are positive, the result will be equal to its contents only.

If the contents are negative, it will add a negative sign to the contents to make it positive.

Now, let us consider the given condition:

`r < 5`

Multiply both sides with 3. (As 3 is a positive number, the equality sign will not change.)

`3r < 15`

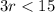
Subtracting 15 from both sides:

`3r-15<15-15\\\Rightarrow 3r-15<0`

Now, we know that
`3r-15<0`, let us use the definition of Modulus function.

Add a negative sign to the contents because the contents are already negative.

`\\\Rightarrow |3r-15| = -(3r-15)\\\Rightarrow -3r+15`

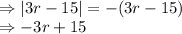
So, the answer is:

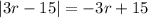`|3r-15| = -3r+15` if
`r<5`