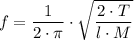Question

On a horizontal frictionless surface a mass M is attached to two light elastic strings both having length l and both made of the same material. The mass is displaced by a small displacement Δy such that equal tensions T exist in the two strings, as shown in the figure. The mass is released and begins to oscillate back and forth. Assume that the displacement is small enough so that the tensions do not change appreciably. (a) Show that the restoring force on the mass can be given by F = -(2T∆y)/l (for small angles) (b) Derive an expression for the frequency of oscillation.

Answer 1

(a) By small angle approximation, we have;

F = -2×T×Δy/l

(b)
`The \ frequency \ of \ oscillation, \ f = (1)/(2\cdot \pi )\cdot\sqrt{(2 \cdot T)/(l \cdot M) }`

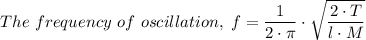
Step-by-step explanation:

(a) The diagram shows the mass, M, being restored by two equal tension, T acting on the elastic strings l, such the restoring force, F acts along the path of motion of the mass, with distance Δy

Therefore, the component of the tension T that form part of the restoring force is given as follows;

Let the angle between the line representing the extension of the elastic strings T and the initial position of the string = ∅

Then we have;

String force,
`F_(string)` = T×sin∅ + T×cos∅ + T×sin∅ - T×cos∅ = 2×T×sin∅

Whereby the angle is small, we have;

sin∅ ≈ tan∅ = Δy/l

Which gives;

`F_(string)` = 2×T×sin∅ = 2×T×Δy/l (for small angles)

Restoring force F =
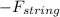`-F_(string)` = -2×T×Δy/l

F = -2×T×Δy/l

(b) Given that the the tensions do not change appreciably as the mass, M, oscillates from Δy we have;

By Hooke's law, F = -k×x

Whereby Δy corresponds to the maximum displacement of the mass, M from the rest position, which gives;

Which gives;

F = M×a = -k×Δy

a = -k×Δy/M

d²(Δy)/dt² = -k×Δy/M

When we put angular frequency as follows;

ω² = k/M

We get;

d²(Δy)/dt² = -ω²×Δy

Which gives;

Δy(t) = A×cos(ωt + Ф)

The angular frequency is thus, ω = √(k/M)

Period of oscillation = 2·π/ω = 2·π/√(k/M)

The frequency of oscillation, f = 1/T = √(k/M)/(2·π)

Where:

k = 2·T/l, we have;

f = √(k/M)/(2·π) = √(2·T/l)/m)/(2·π)

The frequency of oscillation is given as follows;

`f = (1)/(2\cdot \pi )\cdot\sqrt{(2 \cdot T)/(l \cdot M) }`