Question

The automatic opening device of a military cargo parachute has been designed to open when the parachute is 135 m above the ground. Suppose opening altitude actually has a normal distribution with mean value 135 and standard deviation 35 m. Equipment damage will occur if the parachute opens at an altitude of less than 100 m. What is the probability that there is equipment damage to the payload of at least one of five independently dropped parachutes? (Give your answer to four decimal places.)

Answer 1

the probability that there is equipment damage to the payload of at least one of five independently dropped parachutes is 0.4215

Explanation:

Let consider Q to be the opening altitude.

The mean μ = 135 m

The standard deviation = 35 m

The probability that the equipment damage will occur if the parachute opens at an altitude of less than 100 m can be computed as follows:

`P(Q<100) = P((X- 135)/(\sigma) < (100 - 135)/(35)})`

`P(Q<100) = P(z< (-35)/(35)})`

`P(Q<100) = P(z<-1)`

`P(Q<100) = 0.1587`

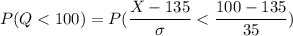
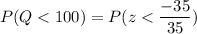
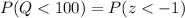
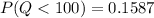
If we represent R to be the number of parachutes which have equipment damage to the payload out of 5 parachutes dropped.

The probability of success = 0.1587

the number of independent parachute n = 5

the probability that there is equipment damage to the payload of at least one of five independently dropped parachutes can be computed as:

P(R ≥ 1) = 1 - P(R < 1)

P(R ≥ 1) = 1 - P(R = 0)

The probability mass function of the binomial expression is:

P(R ≥ 1) =
`1 - (^5_0)(0.1587)^0(1-0.1587)^(5-0)`

P(R ≥ 1) =
`1 - ((5!)/((5-0)!))(0.1587)^0(1-0.1587)^(5-0)`

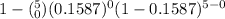
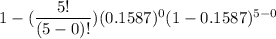
P(R ≥ 1) = 1 - 0.5785

P(R ≥ 1) = 0.4215

Hence, the probability that there is equipment damage to the payload of at least one of five independently dropped parachutes is 0.4215