Question

If possible, find AB, BA, and A2.

Answer 1

First product:

`AB=\begin{bmatrix}3&-3\\-7&0\\2&4\end{bmatrix}\begin{bmatrix}1&0\\0&1\end{bmatrix}=\begin{bmatrix}\begin{bmatrix}3&-3\end{bmatrix}\begin{bmatrix}1\\0\end{bmatrix}&\begin{bmatrix}3&-3\end{bmatrix}\begin{bmatrix}0\\1\end{bmatrix}\\\begin{bmatrix}-7&0\end{bmatrix}\begin{bmatrix}1\\0\end{bmatrix}&\begin{bmatrix}-7&0\end{bmatrix}\begin{bmatrix}0\\1\end{bmatrix}\\\begin{bmatrix}2&4\end{bmatrix}\begin{bmatrix}1\\0\end{bmatrix}&\begin{bmatrix}2&4\end{bmatrix}\begin{bmatrix}0\\1\end{bmatrix}\end{bmatrix}=\begin{bmatrix}3&-3\\-7&0\\2&4\end{bmatrix}`

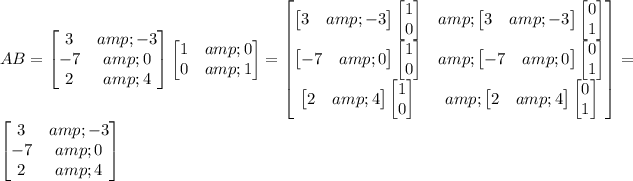
Notice how multiplying A by B produces A again, because B is an identity matrix.

The second product cannot be carried out because A has more columns that B has rows.

The third product also cannot be computed because A is not a square matrix.