Question

Global Airlines operates two types of jet planes: jumbo and ordinary. On jumbo jets, 25% of the passengers are on business while on ordinary jets 30% of the passengers are on business. Of Global's air fleet, 40% of its capacity is provided on jumbo jets. (Hint: The 25% and 30% values are conditional probabilities stated as percentages.) What is the probability a randomly chosen business customer flying with Global is on a jumbo jet?

Answer 1

Answer:

The probability is
`P(J|B) = 0.36`

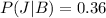
Explanation:

B =business

J=jumbo

Or =ordinary

From the question we are told that

The proportion of the passenger on business in the ordinary jet is
`P(B| Or) = 0.25`

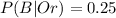
The proportion of the passenger on business in the jumbo jet is
`P(B|J) = 0.30`

The proportion of the passenger on jumbo jets is
`P(j) = 0.40`

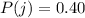
The proportion of the passenger on ordinary jets is evaluated as

`1 - P(J) = 1- 0.40 = 0.60`

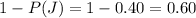
According to Bayer's theorem the probability a randomly chosen business customer flying with Global is on a jumbo jet is mathematically represented as

`P(J|B) = (P(J) * P(B|J))/(P(J ) * P(B|J) + P(Or ) * P(B|Or))`

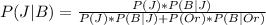
substituting values

`P(J|B) = ( 0.4 * 0.25)/(0.4 * 0.25 + 0.6 * 0.3)`

`P(J|B) = 0.36`

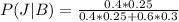
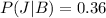
Explanation: