Answer:
AB = 5.6 cm
Explanation:
To find the length of side AB, which is one of the sides of right angled triangle ABC given above, we would apply the trigonometric ratio formula.
The given angle (θ) = 62°
Length of hypotenuse = BC = 12 cm
Length of adjacent side = AB = ?
We would use the following trigonometric ratio formula:
Cos(θ) = adjacent/hypotenuse
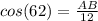
Multiply both sides by 12 to make AB the subject of formula
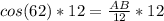
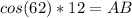
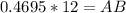
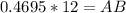
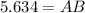
Length of side AB = 5.6 cm (approximated to 1 decimal place)