Question

A statistical program is recommended.

The following observations are on stopping distance (ft) of a particular truck at 20 mph under specified experimental conditions.

32.1 30.9 31.6 30.4 31.0 31.9

The report states that under these conditions, the maximum allowable stopping distance is 30. A normal probability plot validates the assumption that stopping distance is normally distributed.

Required:
a. Does the data suggest that true average stopping distance exceeds this maximum value? Test the appropriate hypotheses using α= 0.01.
b. Calculate the test statistic and determine the P-value.
c. What can you conclude?

Answer 1

We conclude that the true average stopping distance exceeds this maximum value.

Explanation:

We are given the following observations that are on stopping distance (ft) of a particular truck at 20 mph under specified experimental conditions.;

X = 32.1, 30.9, 31.6, 30.4, 31.0, 31.9.

Let
`\mu` = true average stopping distance

So, Null Hypothesis,
`H_0` :
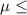`\mu \leq` 30 {means that the true average stopping distance exceeds this maximum value}

Alternate Hypothesis,
`H_A` :
`\mu` > 30 {means that the true average stopping distance exceeds this maximum value}

The test statistics that will be used here is One-sample t-test statistics because we don't know about population standard deviation;

T.S. =
`(\bar X-\mu)/((s)/(√(n) ) )` ~
`t_n_-_1`

where,
`\bar X` = sample mean stopping distance =
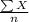`(\sum X)/(n)` = 31.32 ft

s = sample standard deviation =
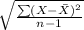`\sqrt{(\sum (X-\bar X)^(2) )/(n-1) }` = 0.66 ft

n = sample size = 6

So, the test statistics =
`(31.32-30)/((0.66)/(√(6) ) )` ~
`t_5`

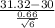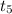
= 4.898

The value of t-test statistics is 4.898.

Now, at 0.01 level of significance, the t table gives a critical value of 3.365 at 5 degrees of freedom for the right-tailed test.

Since the value of our test statistics is more than the critical value of t as 4.898 > 3.365, so we have sufficient evidence to reject our null hypothesis as it will fall in the rejection region.

Therefore, we conclude that the true average stopping distance exceeds this maximum value.