Question

Find the zeros of the function. enter the solutions from least to greatest f(x)=(x+3)^2-4​

Answer 1

x= -5, -1

Explanation:

To find the zeroes of a function,

First expand the terms to get the form
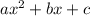`ax^(2) + bx +c` where 'a, b, and c' are constants

`f(x)= (x+3)^(2) -4`

`f(x)= x^(2)+6x+9-4`

`f(x)= x^(2) +6x +5`

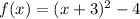
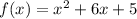
Now, factor the equation

This can be done using the quadratic formula or other methods

One simple method is to find the two values that would get:

• A sum that's equal to the 'b' value and,
• A product that's equal to the 'c' value

A good way to verify is to expand the terms and make sure the function looks the same

In this case, the equation can broken into

f(x)= (x+1)*(x+5)

Now, look at each term individually and set each of them to equal 0

x+1 =0

x+5=0

Solve for x in each case

x= -1

x= -5

Now, ordering them from least to greatest would be: x= -5, -1