Question

The mean student loan debt for college graduates in Illinois is $30000 with a standard deviation of $9000. Suppose a random sample of 100 college grads in Illinois is collected. What is the probability that the mean student loan debt for these people is between $31000 and $33000?

Answer 1

the probability that the mean student loan debt for these people is between $31000 and $33000 is 0.1331

Explanation:

Given that:

Mean = 30000

Standard deviation = 9000

sample size = 100

The probability that the mean student loan debt for these people is between $31000 and $33000 can be computed as:

`P(31000 < X < 33000) = P( X \leq 33000) - P (X \leq 31000)`

`P(31000 < X < 33000) = P( (X - 30000)/((\sigma)/(√(n))) \leq (33000 - 30000)/((9000)/(√(100))) )- P( (X - 30000)/((\sigma)/(√(n))) \leq (31000 - 30000)/((9000)/(√(100))) )`

`P(31000 < X < 33000) = P( Z \leq (33000 - 30000)/((9000)/(√(100))) )- P(Z \leq (31000 - 30000)/((9000)/(√(100))) )`

`P(31000 < X < 33000) = P( Z \leq (3000)/((9000)/(10))}) -P(Z \leq (1000)/((9000)/(10))})`

`P(31000 < X < 33000) = P( Z \leq 3.33)-P(Z \leq 1.11})`

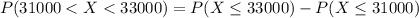
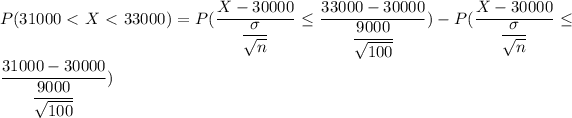
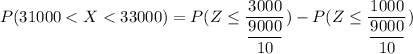
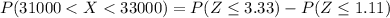
From Z tables:

`P(31000 < X <33000) = 0.9996 -0.8665`

`P(31000 < X <33000) = 0.1331`

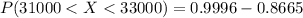
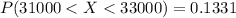
Therefore; the probability that the mean student loan debt for these people is between $31000 and $33000 is 0.1331