Question

El cuadruple de un número aumentado en 2 es menor igual a 50

Answer 1

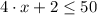`4\cdot x + 2 \leq 50`. La solución de la inecuación es todo número real menor o igual a 12.

Explanation:

El primer paso consiste en traducir la expresión en una expresión algebraica:

1) Un número:
`x`

2) El cuádruplo de un número:
`4\cdot x`

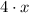
3) El cuádruplo de un número y aumentado en 2:
`4\cdot x + 2`

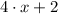
4) El cuádruplo de un número y aumentado en 2 es menor o igual que 50:
`4\cdot x + 2 \leq 50`

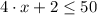
Como siguiente paso, se resuelve la inecuación por métodos algebraicos:

1)
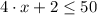`4\cdot x + 2 \leq 50` Dado

2)
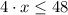`4\cdot x \leq 48` Compatibilidad con la adición/Existencia del inverso aditivo/Modulatividad en la adición.

3)
`x \leq 12` Compatibilidad con la multiplicación/Existencia del inverso multiplicativo/Modulatividad en la multiplicación/Resultado.

En consecuencia, la solución de la inecuación es todo número real menor o igual a 12.