Question

Find the indefinite integral by using the substitution x = 4 sec(θ). (Use C for the constant of integration.) x2 − 16 x d

Answer 1

`(x^2-16)/(2) + 16ln(4)/(x) +16C`

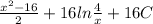
Explanation:

Given the indefinite integral
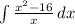`\int\limits{(x^2-16)/(x) } \, dx`, using the substitute

x = 4 sec(θ)...1

The integral can be calculated as thus;

First let us diffrentiate the substitute function with respect to θ

dx/dθ = 4secθtanθ

dx = 4secθtanθdθ... 2

Substituting equation 1 and 2 into the integral function we will have;

`\int\limits{((4sec \theta)^2-16)/(4sec \theta) } \, 4sec \theta tan \theta d \theta\\\int\limits{(16sec^2 \theta-16)/(4sec \theta) } \, 4sec \theta tan \theta d \theta\\\int\limits{((16(sec^2 \theta-1))/(4sec \theta) } \, 4sec \theta tan \theta d \theta\\\\from \ trig \ identity,\ sec^2 \theta - 1 = tan^\theta\\\\\int\limits{(16 tan^2 \theta)/(4sec \theta) } \, 4sec \theta tan \theta d \theta\\\\\int\limits 16 tan^3 \theta d \theta\\\\`

Find the remaining solution in the attachment.