Answer:
P(X ≥ 5) = 0.99972
Explanation:
From the given data;

Mean
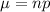
Mean
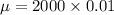
Mean
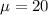
Standard deviation
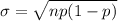
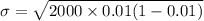

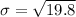
 4.44972
4.44972
P(X ≥ 5) ; The discrete distribution by continuous normal distribution for P(X ≥ 5) lies between 4.5 and 5.5. Hence, Normal distribution x = 4.5 since greater than or equal to is 5 relates to it.
Now;
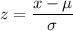
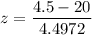
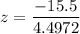
z = −3.45
P(X > 4.5) = P(Z > -3.45)
P(X > 4.5) = 1 - P (Z < - 3.45)
From Normal Z tables;
P(X > 4.5) = 1 - 0.00028
P(X > 4.5) = 0.99972
P(X ≥ 5) = 0.99972