Question

2.CommerceThe weight distribution of parcels sent in a certain manner is normal with meanvalue 12 pounds and standard deviation 3.5 pounds. The parcel service wishes to establish aweight valuecbeyond which there will be a surcharge. What value ofcis such that 99% ofall parcels are under the surcharge weight

Answer 1

the value of c is 20.155 such that 99% of all parcels are under the surcharge weight.

Explanation:

Given that :

The mean value
`\mu` = 12

The standard deviation
`\sigma` = 3.5

Let Consider Q to be the weight of the parcel that is normally distributed .

Then;

Q
`\sim` Norm(12,3.5)

The objective is to determine thewight value of c under which there is a surcharge

Also, let's not that 99% of all the parcels are below the surcharge

However ;

From the Percentiles table of Standard Normal Distribution;

At 99th percentile; the value for Z = 2.33

The formula for the Z-score is:

`Z = (X- \mu)/(\sigma)`

`2.33 = (X - 12)/(3.5)`

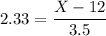
2.33 × 3.5 = X - 12

8.155 = X - 12

- X = - 12 - 8.155

- X = -20.155

X = 20.155

the weight value of c under which there is a surcharge = X + 1 (0) since all the pounds are below the surcharge

c = 20.155 + 1(0)

c = 20.155

Thus ; the value of c is 20.155 such that 99% of all parcels are under the surcharge weight.