Question

Prove the formula for (d/dx)(cos−1(x)) by the same method as for (d/dx)(sin−1(x)). Let y = cos−1(x). Then cos(y) = and 0 ≤ y ≤ π ⇒ −sin(y) dy dx = 1 ⇒

Answer 1

`(d(cos^(-1)x ))/(dx) = (-1)/(√(1-x^2) )`

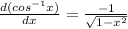
Explanation:

Given the differential (d/dx)(cos−1(x)), to find the equivalent formula we will differentiate the inverse function using chain rule as shown below;

let;

`y = cos^(-1) x \\\\taking \ cos\ of\ both\ sides\\\\cosy = cos(cos^(-1) x)\\\\cosy = x\\\\x = cosy\\\\(dx)/(dy) = -siny\\`

`(dy)/(dx) = (-1)/(sin y) \\\\from\ trigonometry\ identity,\ sin^(2) x+cos^(2)x = 1\\sinx = \sqrt{1-cos^(2) x}`

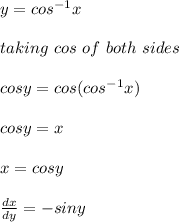
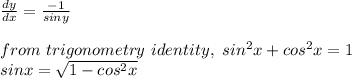
Therefore;

`(dy)/(dx) = \frac{-1}{\sqrt{1-cos^(2)y } }`

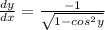
Since x = cos y from the above substitute;

`(dy)/(dx) = \frac{-1}{\sqrt{1-x^(2)} }`

Hence,
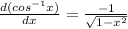`(d(cos^(-1)x ))/(dx) = (-1)/(√(1-x^2) )` gives the required proof