Question

Approximate the change in the volume of a sphere when its radius changes from r​ = 40 ft to r equals 40.05 ft (Upper V (r )equals four thirds pi r cubed ). When r changes from 40 ft to 40.05 ​ft, Upper DeltaValmost equals nothing ftcubed.

Answer 1

The change in the volume of a sphere whose radius changes from 40 feet to 40.05 feet is approximately 1005.310 cubic feet.

Explanation:

The volume of the sphere (
`V`), measured in cubic feet, is represented by the following formula:

`V = (4\pi)/(3)\cdot r^(3)`

Where
`r` is the radius of the sphere, measured in feet.

The change in volume is obtained by means of definition of total difference:

`\Delta V = (\partial V)/(\partial r)\Delta r`

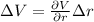
The derivative of the volume as a function of radius is:

`(\partial V)/(\partial r) = 4\pi \cdot r^(2)`

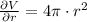
Then, the change in volume is expanded:

`\Delta V = 4\pi \cdot r^(2)\cdot \Delta r`

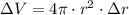
If
`r = 40\,ft` and
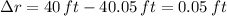`\Delta r = 40\,ft-40.05\,ft = 0.05\,ft`, the change in the volume of the sphere is approximately:

`\Delta V \approx 4\pi\cdot (40\,ft)^(2)\cdot (0.05\,ft)`

`\Delta V \approx 1005.310\,ft^(3)`

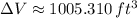
The change in the volume of a sphere whose radius changes from 40 feet to 40.05 feet is approximately 1005.310 cubic feet.