Question

A normally distributed population of package weights has a mean of 63.5 g and a standard deviation of 12.2 g. XN(63.5,12.2) a. What percentage of this population weighs 66 g or more

Answer 1

The percentage is %z
`= 41.9`%

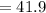Explanation:

From the question we are told that

The mean is
`\mu = 63.5 \ g`

The standard deviation is
`\sigma = 12.2 \ g`

The random number is x = 66 g

Given the the population is normally distributed

The probability is mathematically represented as

`P(X > 66 ) = P((X - \mu )/(\sigma) > (x - \mu )/(\sigma ) )`

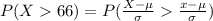
Generally the z-score for this population is mathematically represented as

`Z = ( X - \mu)/( \sigma)`

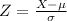
So

`P(X > 66 ) = P(Z > (66 - 63.5 )/(12.2 ) )`

`P(X > 66 ) = P(Z > 0.2049 )`

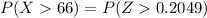
Now the z-value for 0.2049 from the standardized normal distribution table is

`z = 0.41883`

=>
`P(X > 66 ) = 0.41883`

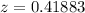
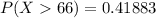
The percentage is

% z
`= 0.41883 * 100`

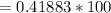
%z
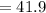`= 41.9`%