Solve each equation for 0 x 360 sqrt 2 cosx+1=0 please hurry

Question

asked Sep 25, 2021 66.6k views

2 Answers

InteXX · Answer 1 · 2021-09-28T04:32:45+0000

Answer:

$120\º \text{ and } 240\º$

or in radians:

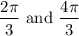
$(2\pi )/(3) \text{ and } (4\pi )/(3)$

Explanation:

From the way you wrote, you want to solve the equation

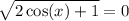$\sqrt {2 \cos(x)+1}=0$ for
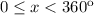$0 \leq x < 360\º$ , or in radians
$[0, 2\pi)$

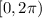
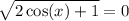
$\sqrt {2 \cos(x)+1}=0$

Square both sides

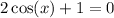
$2 \cos(x) +1= 0$

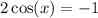
$2\cos(x)=-1$

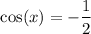
$\cos(x)=-(1)/(2)$

In the Unit Circle, considering one revolution (interval
$[0, 2\pi)$ ),

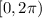the values where
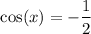$\cos(x)=-(1)/(2)$ are in Quadrant II and III.

Once

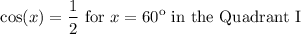
$\cos(x)= (1)/(2) \text{ for } x = 60\º \text{ in the Quadrant I}$

The values where

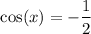$\cos(x)=-(1)/(2)$ are 120º and 240º.