Question

A tungsten filament used in a flashlight bulb operates at 0.20 A and 3.0 V. If its resistance at 20°C is 1.5Ω, what is the temperature of the filament when the flashlight is on?

Answer 1

The temperature of the filament when the flashlight is on is 2020 °C.

Step-by-step explanation:

The resistivity varies linearly with temperature:

`R = R_(0)[1 + \alpha*(T-T_(0))]` (1)

Where:

T: is the temperature of the filament when the flashlight is on=?

T₀: is the initial temperature = 20 °C

α: is the temperature coefficient of resistance = 0.0045 °C⁻¹

R₀: is the resistance at T₀ = 1.5 Ω

When V = 3.0 V, R is:

`R = (V)/(I) = (3.0 V)/(0.20 A) = 15 \Omega`

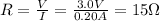
By solving equation (1) for T we have:

`T = (R-R_(0))/(\alpha*R_(0)) + T_(0) = (15-1.5)/(0.0045*1.5) + 20 = 2020 ^(\circ) C`

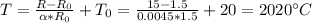
Therefore, the temperature of the filament when the flashlight is on is 2020 °C.

I hope it helps you!