Answer: 1:5
Explanation:
Given: The cost of every mirror is proportional to the cube of the mirror's radius.
i.e.
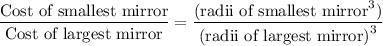
Their largest mirrors have radii of 5 meters and their smallest mirrors have radii of 1 meter.
Then,
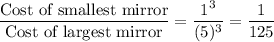
The ratio of the total cost of 25 of the company's smallest mirrors to the cost of one of the company's largest mirrors will be:
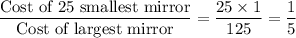
Hence, the ratio of the total cost of 25 of the company's smallest mirrors to the cost of one of the company's largest mirrors = 1:5 .