Answer:
The distance between the ships is changing at 42.720 kilometers per hour at 4:00 PM.
Explanation:
Vectorially speaking, let assume that ship A is located at the origin and the relative distance of ship B with regard to ship A at noon is:

Where
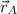 and
and
 are the distances of ships A and B with respect to origin.
are the distances of ships A and B with respect to origin.
By supposing that both ships are travelling at constant speed. The equations of absolute position are described below:
![\vec r_(A) = \left[\left(40\,(km)/(h) \right)\cdot t\right]\cdot i](https://img.qammunity.org/2021/formulas/mathematics/college/5rmnvnpc0z4fdz98aryioku4638vr99p3v.png)
![\vec r_(B) = \left(170\,km\right)\cdot i +\left[\left(15\,(km)/(h) \right)\cdot t\right]\cdot j](https://img.qammunity.org/2021/formulas/mathematics/college/oj6u7hpfwnky1pmqi60i0bx9x28ts2k993.png)
Then,
![\vec r_(B/A) = (170\,km)\cdot i +\left[\left(15\,(km)/(h) \right)\cdot t\right]\cdot j-\left[\left(40\,(km)/(h) \right)\cdot t\right]\cdot i](https://img.qammunity.org/2021/formulas/mathematics/college/x77ceng8l10p8p0j8tbofnood770qpiwax.png)
![\vec r_(B/A) = \left[170\,km-\left(40\,(km)/(h) \right)\cdot t\right]\cdot i +\left[\left(15\,(km)/(h) \right)\cdot t\right]\cdot j](https://img.qammunity.org/2021/formulas/mathematics/college/z7bwloza5aa3xyz70zhtlq1k7scpbimneu.png)
The rate of change of the distance between the ship is constructed by deriving the previous expression:

Its magnitude is determined by means of the Pythagorean Theorem:
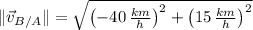
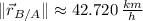
The distance between the ships is changing at 42.720 kilometers per hour at 4:00 PM.