Question

The manager of a grocery store took a random sample of 100 customers. The avg. length of time it took the customers in the sample to check out was 3.1 minutes with a std. deviation of 0.5 minutes. We want to test to determine whether or not the mean waiting time of all customers is significantly > 3 min. At 95% confidence, it can be concluded that the mean of the population is

Answer 1

Explanation:

The data given are;

sample size n = 100

sample mean x = 3.1

standard deviation σ = 0.5

mean = 3

The value for Z can be determined by using the formula:

`Z = (x - \mu)/((\sigma)/(√(n)))`

`Z = (3.1 - 3.00)/((0.5)/(√(100)))`

`Z = (0.1)/((0.5)/(10))}`

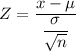
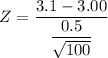
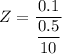
Z = 0.2

At 95% Confidence interval, level of significance ∝ = 0.05

From the z table ;P- value for the test statistics at ∝ = 0.05

P = 0.0228

We can see that the P-value is < ∝

Decision Rule:

Reject the null hypothesis
`H_o` if P-value is less than ∝

Conclusion:

At 0.05 level of significance; we conclude that the mean of the population is significantly > 3 min