Question

1. A survey shows that 15% of nurses are being underpaid in a hospital that employs 200 nurses. (i) Construct a 90% confidence interval to represent the proportion of underpaid nurses in the hospital. Give an interpretation of this interval. [4] (ii) Suppose that in another hospital, 12% of the 120 nurses employed are underpaid. Construct a 90% confidence interval for the difference in proportions of nurses being underpaid at both hospitals. [4]

Answer 1

Answer: (i) Interval for proportion of underpaid nurses: 0.15 ± 0.0415.

(ii) Interval for difference in proportion: 0.03 ± 0.0641

Step-by-step explanation: Confidence Interval for a representation of the proportion is calculated by:

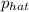`p_(hat)` ± z.
`\sqrt{(p_(hat)(1-p_(hat)))/(n) }`

(i)
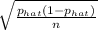
`p_(hat)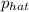` is the proportion, in this case, of underpaid nurses:
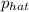`p_(hat)` = 0.15

Confidence Interval is 90%, so z = 1.645

The interval is:

0.15 ± 1.645.
`\sqrt{(0.15(0.85))/(200) }`

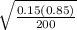
0.15 ± 1.645*0.0252

0.15 ± 0.0415

Which means that, in 90% of times, the proportion of underpaid nurses wil be between 0.1085 and 0.1915.

(ii) For the difference in proportions:

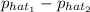`p_(hat_1)-p_(hat_2)` ± z.
`\sqrt{(p_(hat_1)(1-p_(hat_1)))/(n_(1))+(p_(hat_2)(1-p_(hat_2)))/(n_(2)) }`

The proportion for the second hospital is
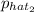`p_(hat_2)` = 0.12 and, since it is the same confidence interval, z = 1.645.

Calculating:

(0.15-0.12) ± 1.645.
`\sqrt{(0.15(0.85))/(200) + (0.12(0.88))/(120) }`

0.03 ± 1.645*0.0389

0.03 ± 0.0641

The 90% confidence interval for the difference in proportions of nurses being underpaid is between 0.0341 and 0.0941