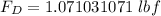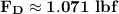Answer:
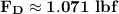
Step-by-step explanation:
Given that:
The height of a triangular stabilizing fin on its stern is 1 ft tall
and it length is 2 ft long.
Temperature = 60 °F
The objective is to determine the drag on the fin when the submarine is traveling at a speed of 2.5 ft/s.
From these information given; we can have a diagrammatic representation describing how the triangular stabilizing fin looks like as we resolve them into horizontal and vertical component.
The diagram can be found in the attached file below.
If we recall ,we know that;
Kinematic viscosity v =
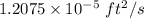
the density of water ρ = 62.36 lb /ft³
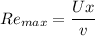
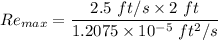

 which is less than < 5.0 × 10⁵
which is less than < 5.0 × 10⁵
Now; For laminar flow; the drag on the fin when the submarine is traveling at 2.5 ft/s can be determined by using the expression:
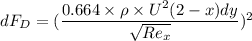
where;
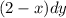 = strip area
= strip area

Therefore;
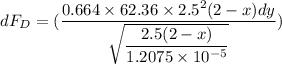
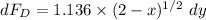
Let note that y = 0.5x from what we have in the diagram,
so , x = y/0.5
By applying the rule of integration on both sides, we have:
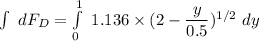
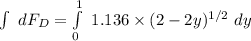
Let U = (2-2y)
-2dy = du
dy = -du/2
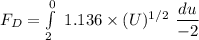
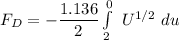
![F_D = -0.568 [ \frac{(1)/(2)U^{ (1)/(2)+1 } }{(1)/(2)+1}]^0__2](https://img.qammunity.org/2021/formulas/engineering/college/57cm08n3wtx350oidfvyup9bbn2w6kz6c8.png)
![F_D = -0.568 [ (2)/(3)U^{(3)/(2) } ] ^0__2](https://img.qammunity.org/2021/formulas/engineering/college/y9q6gisv4l8zj4xu2ot1g21btic3fwghgl.png)
![F_D = -0.568 [0 - (2)/(3)(2)^{(3)/(2) } ]](https://img.qammunity.org/2021/formulas/engineering/college/5svn3m548q17gr1g3taualk7657sshg6vx.png)
![F_D = -0.568 [- (2)/(3) (2.828427125)} ]](https://img.qammunity.org/2021/formulas/engineering/college/mw86v326zzecs913m6hyara0zofju1u2a6.png)