Answer:
0.9855 or 98.55%.
Explanation:
The probability of each individual match being flawed is p = 0.008. The probability that a matchbox will have one or fewer matches with a flaw is the same as the probability of a matchbox having exactly one or exactly zero matches with a flaw:
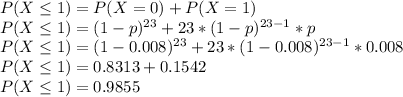
The probability that a matchbox will have one or fewer matches with a flaw is 0.9855 or 98.55%.