Answer:
498 m
Explanation:
The AAA theorem states that triangles are similar if all three corresponding angles are equal.
1. Compare triangles FHS and ILS
(a) Reason for similarity
∠F = ∠I = 90°
∠S is common.
∴ ∠H = ∠L
(b) Calculate SL

2. Compare triangles ILS and GLE
(a) Reason for similarity
∠I = ∠G = 90°
∠L is common.
∴ ∠S = ∠E
(b) Calculate LE
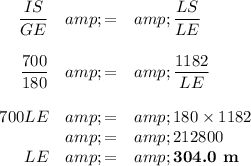
3. Calculate EH
LE + EH + HS = LS
304.0 m + EH + 380 m = 1182 m
EH + 684 m = 1182 m
EH = 498 m
The distance from E to H is 498 m.