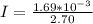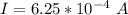Question

A flat loop of wire consisting of a single turn of cross-sectional area 8.20 cm2 is perpendicular to a magnetic field that increases uniformly in magnitude from 0.500 T to 2.60 T in 1.02 s. What is the resulting induced current if the loop has a resistance of 2.70

Answer 1

The induced current is
`I = 6.25*10^(-4) \ A`

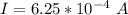
Step-by-step explanation:

From the question we are told that

The number of turns is
`N = 1`

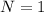
The cross-sectional area is
`A = 8.20 cm^2 = 8.20 * 10^(-4) \ m^2`

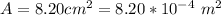
The initial magnetic field is
`B_i = 0.500 \ T`

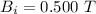
The magnetic field at time = 1.02 s is
`B_t = 2.60 \ T`

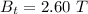
The resistance is
`R = 2.70\ \Omega`

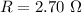
The induced emf is mathematically represented as

`\epsilon = - N * ( d\phi )/(dt)`

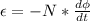
The negative sign tells us that the induced emf is moving opposite to the change in magnetic flux

Here
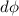`d\phi` is the change in magnetic flux which is mathematically represented as

`d \phi = dB * A`

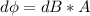
Where dB is the change in magnetic field which is mathematically represented as

`dB = B_t - B_i`

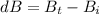
substituting values

`dB = 2.60 - 0.500`

`dB = 2.1 \ T`

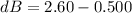
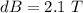
Thus

`d \phi = 2.1 * 8.20 *10^(-4)`

`d \phi = 1.722*10^(-3) \ weber`

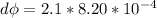
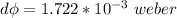
So

`|\epsilon| = 1 * ( 1.722*10^(-3))/(1.02)`

`|\epsilon| = 1.69 *10^(-3) \ V`

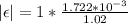
The induced current i mathematically represented as

`I = (\epsilon)/( R )`

substituting values

`I = (1.69*10^(-3))/( 2.70 )`

`I = 6.25*10^(-4) \ A`