Question

F(x) = 4x^4 – 2x^3 – 3x^2 + 6x - 9 Find the Zeros Using Descartes' Rule of Signs

Answer 1

So possibilities of zeroes are:

Positive Negative Imaginary

1 1 2

3 1 0

Zeroes = -1.4549, 1.2658, 0.34457-1.0503i, 0.34457+1.0503i.

Explanation:

Note: Descartes' Rule of Signs is used to find the signs of zeroes not the exact value.

The given function is

`f(x)=4x^4-2x^3-3x^2+6x-9`

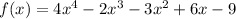
Degree of polynomial is 4 so number of zeroes is 4.

There are three sign changes, so there are either 3 positive zeros or 1 positive zero.

Now, put x=-x in f(x).

`f(-x)=4(-x)^4-2(-x)^3-3(-x)^2+6(-x)-9`

`f(-x)=4x^4+2x^3-3x^2-6x-9`

There is one variation in sign change, so there is 1 negative zero.

So possibilities of zeroes are:

Positive Negative Imaginary

1 1 2

3 1 0

Using graphing calculator the zeroes of given function are -1.4549, 1.2658, 0.34457-1.0503i and 0.34457+1.0503i.