Answer:
Explanation:
Let x be the number of 2 coins and y be the number of 5 coins. Let z be the number of 10 coins she exchanged. Then, we have the first equation
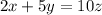
Since she has one 5 coin less than 2 coins, then y=x-1. So we get the equation

which is equivalent to
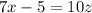
If we add 5 on both sides and factor out on the right by 5 we get
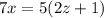
We can solve for x and get

Since x represents the number of 2 coins, we must have that x is an integer. That is, we cannot have, for example 1.5 2 coins. Since 7 doesn't divide 5, we must have that 7 divides 2z+1. That is, the value of z is such that the number 2z+1 is multiple of 7. That is 2z+1 = 7p where p is an integer.
If that is the case, then
x = 5p, then y = 5p-1. By having 2z+1 = 7p, we are forcing that p is an odd integer, so we have infinite solutions. For each value of p that is an odd integer, then x=5p and y=5p-1 is a solution to the problem