we have that
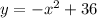
we know that
Is the equation of a vertical parabola open down
so
the vertex is a maximum
step 1
convert the equation of the parabola in the vertex form
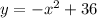
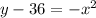
the vertex (h,k) is the point (0,36)
Part a) The point on the graph where the height of the tunnel is a maximum is (0,36)
Part b) The points on the graph where the height of the tunnel is zero feet is when y=0
so
for y=0
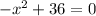
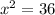
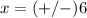
the points are (-6,0) and (6,0)
see the attached figure